Many of us have heard the adage that if you double a penny every day, it will grow into a substantial amount over time.
This concept, although simple, exemplifies the power of exponential growth.
In this article, we will delve into the penny-doubled phenomenon, exploring it over various time frames: 15 days, 30 days, 365 days, and 10 years.
The Penny Doubled: Exponential Growth Explained
The penny-doubled concept represents an exponential growth scenario.
Simply put, if you start with a single penny and double its value each day, the total amount grows exponentially rather than linearly.
The formula is straightforward:
Total amount = initial amount * (2^(number of days) - 1)
The ‘^’ symbol denotes the exponent, meaning you multiply the initial amount by 2, raised to the power of the number of days.
Starting with an initial amount of one penny, the formula becomes:
Total amount = $0.01 * (2^(number of days) - 1)
With this formula in mind, let’s explore the growth of a penny doubled over various periods.
Penny Doubled for 15 Days
Using the penny-doubled formula, we find that after 15 days of doubling a penny, you end up with:
Total amount = $0.01 * (2^14) = $327.68
It’s impressive to see how a single cent, when doubled daily, can grow to over $300 in just half a month.
But the real power of exponential growth becomes more evident when we expand the time frame.
Penny Doubled for 30 Days
After 30 days of doubling, the penny’s growth becomes truly astonishing:
Total amount = $0.01 * (2^29) = $5,368,709.12In just one month, a penny, if doubled each day, would surpass $5 million.
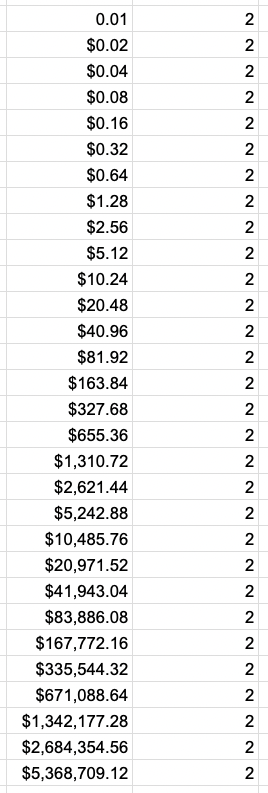
This dramatic increase demonstrates the powerful impact of exponential growth over time.
Penny Doubled for 365 Days
At this point, you may be wondering, “What if we continued to double the penny over an entire year?”
The result is mind-boggling.
Plugging 365 into our formula gives:
Total amount = $0.01 * (2^364)
The result is a number so large that it’s hard to comprehend: over 4 quintillion dollars (that’s 4 followed by 18 zeros).
This number exceeds the global economy, illustrating the power—and limitations—of exponential growth.
Realistically, such growth can’t be sustained indefinitely due to various practical constraints.
Penny Doubled for 10 Years
Carrying on with our theoretical exercise, if we were to double a penny every day for 10 years (or approximately 3,650 days), the resulting figure becomes astronomical:
Total amount = $0.01 * (2^3650)
The number is so large that it exceeds the total number of atoms estimated to exist in the observable universe.
This shows us the true power of exponential growth, but also illustrates that in practical terms, growth will always be restrained by physical or economic limitations.
$1,000,000? or A penny doubled everyday for 30 days?
Conclusion
The concept of doubling a penny over time showcases the principle of exponential growth.
While the figures can become staggeringly large, and thus unrealistic in real-world terms, understanding this concept is crucial in various fields, including finance and technology, where exponential growth patterns frequently occur.
It also illustrates that for financial portfolios, small contributions can add up to big gains over time.